Lattice-Based Cryptography

Lattice-based cryptography is the most important area of post-quantum cryptography. It is known for its efficiency and versatility, with use cases ranging from the foundational building blocks of cryptography to highly complex protocols.

The National Institute of Standards and Technology (NIST) is standardizing a collection of algorithms through the Post-Quantum Cryptography (PQC) Standardization Process, which will influence the landscape of digital security for the coming decades. NIST is currently in its third round of narrowing the candidate algorithms. The most prominent key establishment and digital signature candidates left in this standardization process are lattice-based.

What are the Advantages of Lattice-Based Cryptography?

1. Standardization: It is highly likely that NIST will standardize at least one lattice-based key establishment algorithm and at least one lattice-based digital signature algorithm between 2022-2024.
2. Speed: The favoured lattice-based algorithms are extremely fast. They are not just faster than other quantum-safe cryptographic algorithms, but in many cases, lattice-based algorithms are also faster than the notoriously fast elliptic curve cryptography.
3. Reasonable Key Sizes: Although not quite as small as classical cryptographic algorithms, or even some of the quantum-safe isogeny-based algorithms, the key sizes of lattice-based cryptography are small enough to use in standard protocols.
4. Heavy Scrutiny: The confidence in the security of a cryptographic algorithm is largely based on the amount of scrutiny the algorithm has undergone. Lattice-based cryptography has existed since the 1990s. Following a substantial increase in popularity in the 2000s, the security of lattice-based cryptography has received a lot of attention and has received more scrutiny than other areas of post-quantum cryptography.
5. Diverse Uses: Lattices allow us to solve a diverse set of security challenges. These include highly practical constructions such as key agreements and signatures schemes. However, lattice-based cryptography has also allowed for more elaborate constructions such as identity-based encryption (IBE) and fully homomorphic encryption (FHE).
6. Mathematical Foundation: For certain parameters there are mathematical relationships that give researchers a high degree of assurance in the security of the resulting cryptosystem. While the leading lattice-based candidates for NIST’s PQC standardization do not choose sufficiently large parameters to mathematically provide these assurances, their designs use these relations as a guideline, and this gives us confidence that they do not have irreparable flaws.
7. Understandablity: As the algorithms in this area are based on linear algebra, less mathematical background is required to obtain a high-level understanding of the algorithms, as compared to, for example, isogeny-based cryptography.

How to Start Using Lattice-Based Cryptography?

Our dedicated team of researchers have scrutinized the lattice-based submissions to NIST’s post-quantum cryptography standardization process and have identified the most promising submissions. Our developers then worked hard to program efficient implementations of these algorithms. They have also integrated these algorithms into OpenSSL. This makes it easier for organizations to evaluate the use of lattice-based cryptography as part of their products and networks

Technical Deep-Dive: More Information on Lattice-Based Algorithms

What are Lattices?

We can visualize a lattice as a multi-dimensional grid, like the one in the following diagram.

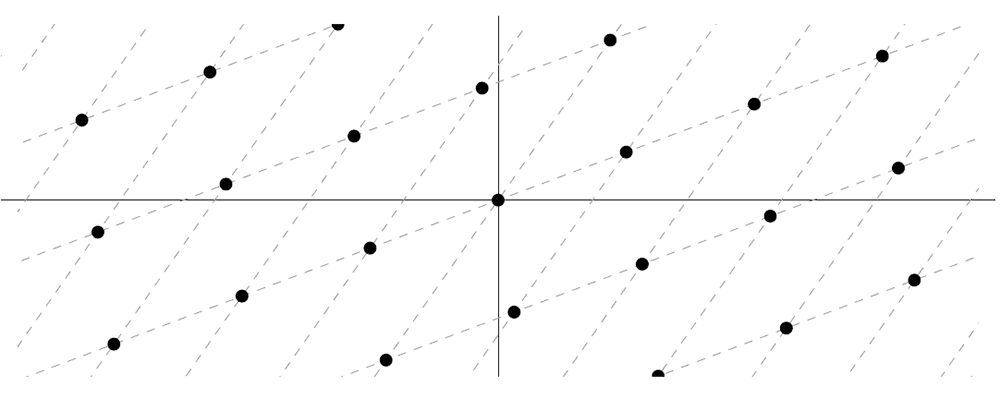
How do these grids allow us to form a cryptographic algorithm? Generally, the security of a cryptosystem is based on one or more hard problems.

Hard problems are ones that can only be efficiently solved if you have some extra secret information. In the case of lattice-based cryptography all the hard problems involve lattices in some way.

One example of a lattice problem that cryptographers believe is hard to solve in general is the following:

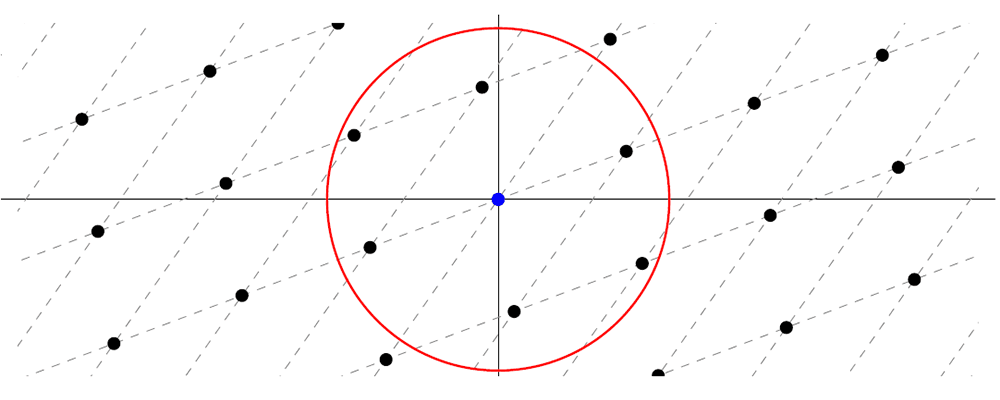
Short Integer Solution Problem (SIS): Suppose we are given a random matrix A with entries between 0 and a number q. The problem is to find a “short” vector x that is a solution to the equation

Ax ≡ 0 (mod q). 

You might wonder how the SIS problem is related to lattices. The set of vectors x that are solutions (of any length) to the equation Ax ≡ 0 ("mod" q) can be plotted in a grid-like structure, i.e., as a lattice. The SIS problem is to find a solution x that is close to, but not equal to, the origin. For example, consider the lattice diagram below. The challenge is to find a point that is within the red circle, but which is not the blue point.

Technical Aside: There are some extra conditions that are needed for this problem to be difficult to solve. For example, if the matrix has certain dimensions, then this problem is trivial to solve. Typically lattice problems are easy to solve in 2-dimensions but become harder to solve as the dimensions increase.

How can we use SIS to create a cryptosystem? It is possible to generate a matrix A together with secret information that makes SIS easy to solve for the owner of the secret information, and hard to solve for anyone else. Furthermore, finding the secret information is also difficult. This idea can be used to create signature schemes (for example, Falcon, a NIST PQC 3rd Round Candidate).

In terms of specific algorithms, Falcon and Dilithium (another NIST PQC 3rd Round Candidate) base their security on hard lattice problems which include the SIS problem.

Another hard problem is the following:

Learning With Errors Problem (LWE): Suppose we are given a random matrix A with entries between 0 and a number q. Further suppose there is an unknown vector s and an unknown “short” vector e. The problem is to find s given only the matrix A and the value sA+e ("mod" q).

The set of all the possible values of xA, where x is allowed to vary, forms a lattice (the blue and black points of the grid illustrated in the diagram below). We can think of the green point in the diagram below as a point of the form b=sA+e that is close to a particular lattice point sA (the blue point). The idea that these two points are close corresponds to the fact that e is a short vector, also known as an error vector.

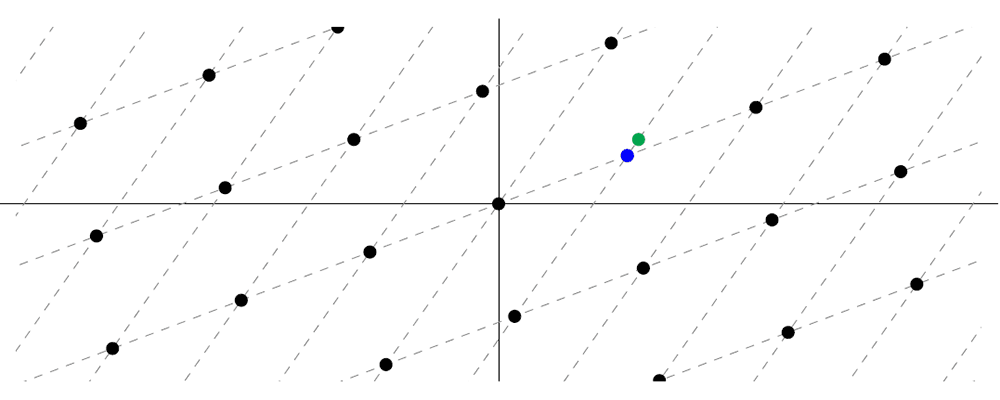
The LWE problem can be intuitively thought as being given a point of the form b=sA+e (the green point) and being asked to find the point on the grid that is close to b (the blue point).

As with SIS, there is information that can make LWE easier to solve, but the information is difficult for anyone to obtain when A is a randomly chosen matrix. For example, the security of many of the NIST PQC candidate key encapsulation mechanisms (Kyber, Saber, and FrodoKEM) and signature algorithms (Dilithium) are based on problems that are related to LWE.

Technical Aside: Sometimes you might see a discussion of a Ring or Module version of LWE, SIS, or another lattice problem. These are basically the same hard problems instantiated over more complex mathematical structures (rings, modules, etc.) for efficiency.

Some of the other schemes (NTRU, NTRU Prime, and Falcon) use a problem called the NTRU problem. On the surface the NTRU problem looks a little different than the above lattice problems, however, the algebraic structures involved can be reinterpreted as lattices.

Overall, the candidates for the NIST post-quantum standardization process are based on many hard problems. However, those based on lattices seem the most promising so far. That being said, other areas of post-quantum cryptography will likely yield algorithms for special use cases which cannot be addressed as well by using lattice-based algorithms. For more details see our blog posts on hash-based cryptography and isogeny-based cryptography.