Math Paths to Quantum-Safe Security: Isogeny-Based Cryptography
By Victoria de Quehen, Security Researcher, ISARA Corporation
Published July 27th, 2018
One of the most widely deployed public key cryptographic algorithms is the elliptic curve Diffie-Hellman key exchange (ECDH). This, as well as most currently used protocols, is vulnerable to attacks using quantum computers. Isogeny-based cryptography offers the closest quantum-safe cryptographic primitives to ECDH.
What are the Main Isogeny-based Algorithms?
A large group of researchers and developers working on isogeny-based cryptography united their efforts to put forth a single submission to NIST’s call for submissions: Supersingular Isogeny Key Encapsulation (SIKE) [4]. This is a key encapsulation mechanism (KEM) that is closely related to the quantum-resistant key agreement Supersingular Isogeny Diffie-Hellman (SIDH) introduced by Jao and De Feo [3].
What are the Advantages of Isogeny-Based Cryptography?
- Small Key Sizes: Isogeny-based algorithms are known for having far smaller key sizes than other quantum-safe protocols. For example, SIKEp751 requires public keys of around 400 bytes to achieve 124-bits of quantum security [4], meanwhile, KYBER768, one of the most promising lattice-based KEM submitted to the NIST competition, requires public keys of over 1000 bytes to achieve 128-bits of quantum security [1].
- Similar to ECDH: SIDH is inspired by ECDH and it has a similar flow. As we will see, SIDH differs from ECDH by replacing the scalar multiplication by isogenies.
- Well-Known Hard Problem: These isogeny-based algorithms are based on a problem involving elliptic curves that is considered to be hard, in an area that has been well-studied by both mathematicians and cryptographers. This problem states that given two elliptic curves it is difficult to calculate an isogeny (a special type of function) between them.
- Completely Different from Other Schemes: Isogeny-based algorithms are sometimes recommended in combination with lattice-based algorithms, as the two different mathematical areas are very far apart. The idea being that if one of the two areas of quantum-safe cryptography becomes vulnerable, the other will still be secure.
- Well-Understood Parameters: The known attacks against the underlying problem are well understood. This makes it easy to choose parameters that are safe. In fact, recent arguments suggest they are more conservative than necessary!
- Large Basis of Expertise: As isogeny-based cryptography uses elliptic curves, the expertise of classical cryptographers that are familiar with these concepts can be transferred to this new area.
- Good Hybrid with ECDH: It is often suggested to combine quantum-safe algorithms with an established classic algorithm. Specifically, for added security, there is a hybrid algorithm that combines SIDH with the heavily scrutinized ECDH. As both use elliptic curves, this can be done efficiently [2].
- Faster Computers: Although SIDH and SIKE are slower than some other cryptosystems, as computers and circuits get faster this will be less important. Some cryptographers believe isogeny-based cryptography will become dominant since bandwidth, especially for embedded devices, historically grows slower than computing power, making the smaller key size compensate for the slower speed.
How you can use Isogeny-based Cryptography
Supersingular Isogeny Diffie-Hellman (SIDH) is a key exchange protocol [3]. It is an algorithm that allows two parties to jointly establish a shared secret key over an insecure channel. You can use SIDH wherever you use ephemeral ECDH or DH. It is implemented in the ISARA Radiate™ 1.4 Toolkit, and using ISARA Radiate’s Open SSL Connector, is integrated into protocols in OpenSSL.
If you are using OpenSSL, then you can use one of our TLS cipher- suites that feature SIDH as a key exchange algorithm. If you are not using OpenSSL, then you can directly call into our toolkit.
Supersingular Isogeny Key Encapsulation (SIKE) is a KEM [4]. It will be implemented in an upcoming release of the ISARA Radiate Toolkit.
Meet Our Isogeny Team
- Victoria de Quehen, Security Researcher
- Kassem Kalach, Security Researcher
- Shane Kelly, Security Developer
- Anton Mosunov, Ph.D. Candidate, Security Researcher
- Chris Leonardi, Ph.D. Candidate, Security Researcher
- Alex Parent, Security Developer
Technical Deep-Dive: More Information on Isogeny-based Algorithms
In SIDH two parties wish to agree upon a key. Its form is similar to that of Diffie-Hellman and Elliptic Curve Diffie-Hellman. Let us first review Elliptic Curve Diffie-Hellman, and then see the differences.
Elliptic Curve Diffie-Hellman (ECDH)
- Both parties start with the same point P on an elliptic curve E.
- Each party chooses a secret number, call one NA and the other NB. One party calculates the scalar multiple of the point P by NA and the other calculates the scalar multiple of P by NB.
- The parties publicly exchange the points which they have calculated ([NA]·P and [NB]·P) while keeping the numbers NA and NB private.
- Both parties can now calculate the shared secret key [NANB] · P = [NBNA] · P, however, an attacker cannot.
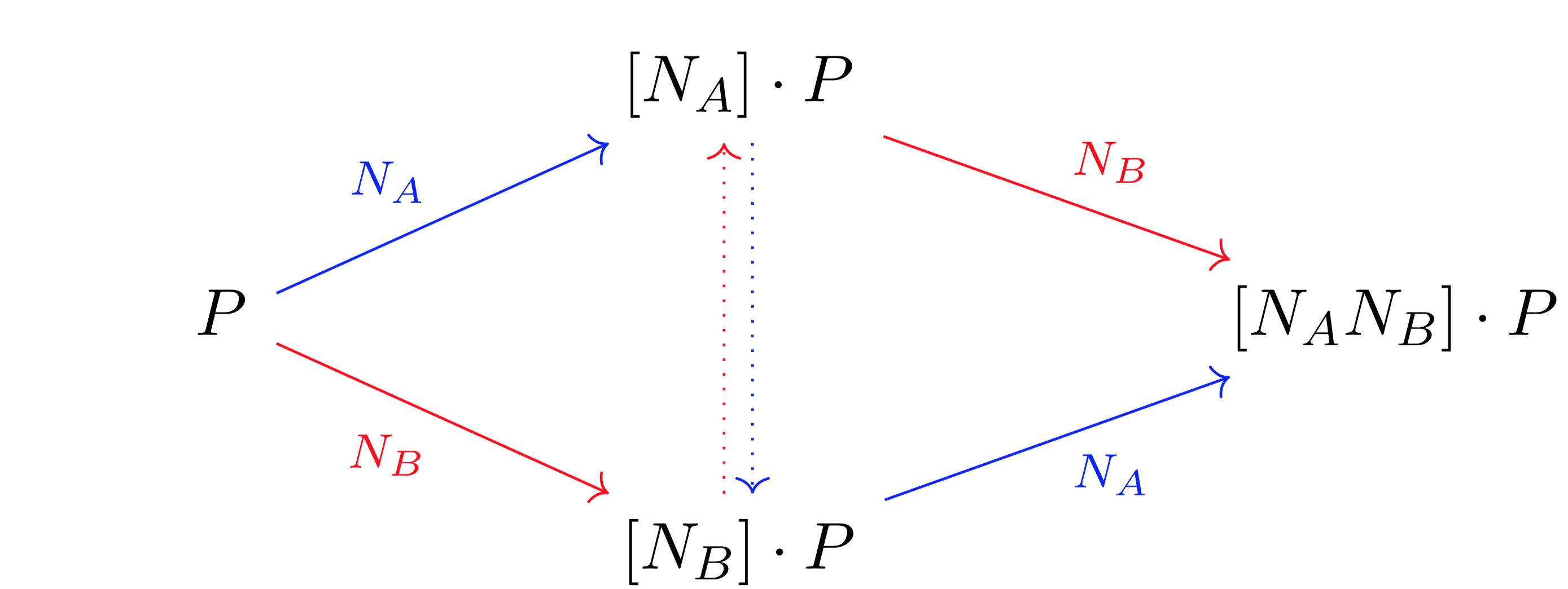
Figure 1: ECDH. Scalar multiplication can be thought of as a function between elliptic curves. One party calculates the arrows in red, and the other party calculates the arrows in blue. The dotted lines represent the parties exchanging the points [NA] · P and [NB] · P.
How is SIDH Different from ECDH?
The main difference is that the scalar multiplication is replaced by a type of function between elliptic curves called an isogeny. Also instead of calculating the image of a point P under two different functions, the parties calculate the image of the entire elliptic curve under the two different functions.
Supersingular Isogeny Diffie-Hellman (SIDH)
- Both parties start with the same elliptic curve E.
- Each party chooses a secret number, call one rA and the other rB. One party creates a function φA from rA and calculates the image curve EA = φA(E). The other party creates a function φB from rB and calculates the image curve EB = φB(E).
- The images curves EA and EB are exchanged publicly, while the numbers rA and rB used to create the functions φA and φB are kept secret.
- The one party now creates a function ψA on EB from their secret key rA, and finds its image ψA(EB). The other party creates a function ψB on EA from their secret key rB, and finds its image ψB(EA). The shared secret key is computable from both ψA(EB) and ψB(EA), but cannot be computed without knowing rA or rB [5].
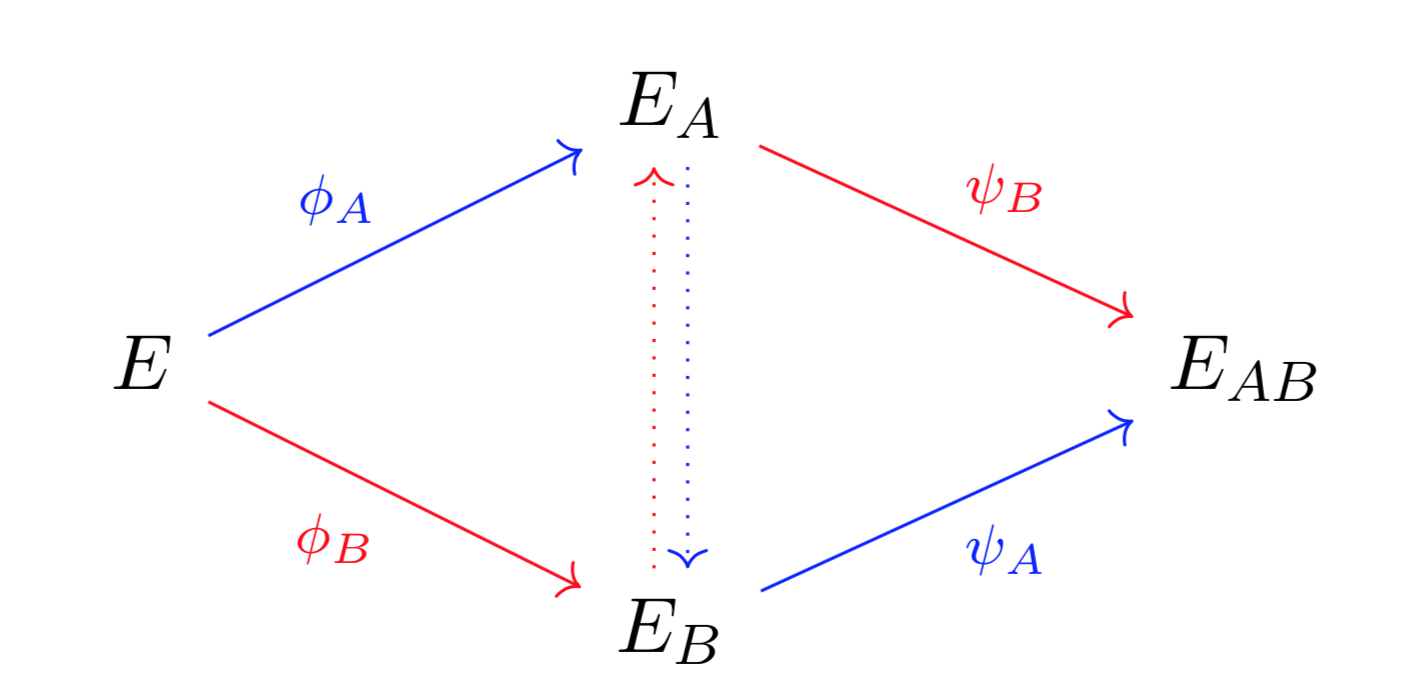
Figure 2: SIDH
Is Isogeny-based Cryptography Really This Simple?
Most descriptions of SIDH and SIKE seem far more complicated. This is because the functions are harder to describe and calculate than with ECDH. Not only are the algorithms for calculating images of isogenies computationally more expensive, but the parties also need to keep track of and exchange certain points on the curve, in order to later calculate the functions ψA and ψB. That being said, the overall framework of SIDH really is very similar to ECDH.
The Hard Problem on which SIDH and SIKE are Based
These algorithms are built on the hard problem of finding isogenies between elliptic curves. Given two elliptic curves, it has long been considered to be extremely difficult to find an isogeny from one elliptic curve to the other. In particular, knowing E, EA and EB are thought to give no information about the isogenies φA and φB. This means that an attacker cannot calculate ψA, ψB or EAB. Therefore an attacker cannot figure out the secret key.
To learn more, check out our Isogeny-Based Cryptography Tutorial here
Bibliography
- [1] Roberto Avanzi, Joppe Bos, Léo Ducas, Eike Kiltz, Tancrède Lepoint, Vadim Lyubashevsky, John M Schanck, Peter Schwabe, Gregor Seiler, and Damien Stehlé. Crystals-kyber algorithm specifications and supporting documentation. NIST Round 1 Submissions for Post-Quantum Cryptography Standardization, 2017.
- [2] Craig Costello, Patrick Longa, and Michael Naehrig. Efficient algorithms for supersingular isogeny Diffie-Hellman. In Annual Cryptology Conference, pages 572–601. Springer, 2016.
- [3] Luca De Feo, David Jao, and Jérôme Plût. Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. Journal of Mathematical Cryptology, 8(3), pages 209–247, 2014.
- [4] David Jao, Reza Azarderakhsh, Matthew Campagna, Craig Costello, Amir Jalali, Brian Koziel, Brian LaMacchia, Patrick Longa, Michael Naehrig, Joost Renes, et al. Supersingular isogeny key encapsulation. NIST Round 1 Submissions for Post-Quantum Cryptography Standardization, 2017.
- [5] David Jao and Luca De Feo. Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. In International Workshop on Post-Quantum Cryptography, pages 19–34. Springer, 2011.
Contact ISARA’s embedded security experts today
If you have further questions, set up a meeting with our team here.
Learn about the other five areas of math used in quantum-safe cryptography in our blog series, “Math Paths to Quantum-Safe Security”:
- Hash-based cryptography
- Lattice-, code-, and multivariate-based to be posted