Math Paths to Quantum-safe Security: Hash-based Cryptography

By Victoria de Quehen, Security Researcher, ISARA Corporation

Published February 24, 2020

Digital signature algorithms are a critical component of public-key infrastructure, with applications ranging from code signing to establishing secure connections. However, classical digital signature algorithms will be vulnerable to quantum-enabled attacks. Hash-based cryptography is among the oldest area of quantum-safe cryptography, with digital signature algorithms dating back to 1979, before the invention of elliptic curve cryptography.

What is the Basic Idea?

In the late 1970’s, Leslie Lamport introduced the idea of a One-Time Signature (OTS)—a signature algorithm that could be used at most once. Although it may not seem practical to use a signature scheme that can only be used at most once, shortly after Lamport’s influential publication, Ralph Merkle turned this seemingly impractical idea into a signature algorithm that could be used many times, and in doing so, gave birth to the first many-time hash-based algorithm.

‘Stateful’ versus ‘Stateless’ Hash-Based Signatures

Hash-based signatures fall into two distinct types: stateful and stateless.

All many-time hash-based signature algorithms work by efficiently combining many instances of OTSs. However, with stateful hash-based signature algorithms, it is vital to not accidentally sign multiple messages with the same OTS signing key. After each signature the state is updated, and this essentially keeps track of which OTS keys have been used. Managing state can be difficult with severe consequences if implemented incorrectly. It is important to make correct architectural decisions (for example, for disaster recovery) to safely manage state if there are multiple pieces of hardware or equipment that have to work together. For this reason, we recommend working with companies with expertise in stateful hash-based cryptography.

There are also stateless hash-based signatures, that do not require managing a state, and are far easier to implement. Unfortunately, stateless signatures are far less efficient: the signatures are much larger and they are computationally more intensive. As well, stateless signatures are still 2-4 years away from standardization. On the other hand, stateful hash-based algorithms are expected to be standardized within a year, and with real-world expertise they can be implemented safely.

What are the Main Hash-Based Signature Schemes?

Hash-based cryptography was first developed by Leslie Lamport and Ralph Merkle in the late 1970s. Since Merkle’s original scheme [5], hash-based algorithms have become much more efficient. The leading contenders for post-quantum hash-based signatures are the stateful algorithms Multi-Tree eXtended Merkle Signature Scheme (XMSS^MT) [3] and Hierarchical Signature System (HSS) [4], and the stateless algorithm SPHINCS+ [2].

Are there Standards for Hash-Based Signature Schemes?

A major advantage of hash-based signatures is a high degree of confidence in their mathematical security. Unlike other quantum-safe cryptographic algorithms which are 2-4 years away from being standardized, the stateful hash-based signature schemes XMSS^MT and HSS have been studied and approved by the Crypto Forum Research Group (CFRG) and published as RFC 8391[3] and RFC 8554 [4], respectively.

Although CFRG RFC’s are not technically considered to be standards, the National Institute of Standards and Technology (NIST) has recently published a draft Special Publication (NIST SP 800-208 [1]) which, when finalized, will serve as a national standard for XMSS^MT and HSS. As is common with NIST standards, this special publication will likely become a de facto international standard as well.

Why is Hash-Based Cryptography Secure?

Hash-based cryptography creates signature algorithms whose security is mathematically based on the security of a selected cryptographic hash function.

Consider, for example, NIST’s set of well-trusted and ubiquitous cryptographic hash functions Secure Hash Algorithm 2 (SHA-2). SHA-2 is considered to be secure against attacks by adversaries having access to today’s most powerful supercomputers, and it is believed to be quantum-safe as well. This means a hash-based signature algorithm that uses SHA-2 is essentially as secure as SHA-2, which is to say, extremely secure.

Moreover, even in the unlikely event that SHA-2 is compromised, the security of hash-based signatures could be restored simply by switching to another uncompromised hash function. Systems like these hash-based signatures, where switching between algorithms has a low cost, are referred to as crypto-agile.

How can you use Hash-Based Cryptography?

Use cases that require immediate action could in many cases benefit from a hash-based solution. For example, many long-lived connected devices, especially ones that operate in hard-to-reach locations, such as satellites, will need security well after large-scale quantum computers are likely to exist.

For this reason, these devices could benefit from an approved hash-based digital signature algorithm. Such algorithms can be integrated now, to avoid financially prohibitive or logistically impossible upgrades in the future.

Advantages of Hash-Based Cryptography

1. Security: The security of hash-based signature algorithms is based on the security of highly trusted hash functions, like SHA-2.
2. Standardization: Stateful hash-based signature algorithms will likely be standardized by NIST within the year, and for this reason, they provide the best solution for critical assets that require urgent action.
3. Utilizes Current Hardware: Unlike other areas of quantum-safe cryptography (which rely on new types of mathematics), the majority of the calculations done in hash-based signature algorithms involve computing hash functions. For most of the NIST approved hash functions, these computations have already been optimized in hardware, making hash-based implementations in long-lived connected devices more practical.
4. Small Public Key: The public key can be extremely small relative to other post quantum signature schemes, (smaller than 128 bytes). To compare this to other post-quantum signature schemes look at our Toolkit documentation.
5. Small Secret Key: By storing less information (of the Merkle tree described in the Deep-Dive Section below) we can reduce the size of the private keys. In fact, we can reduce the private key size further by using a single (32 byte) seed to generate multiple values.
6. Time/Space Tradeoffs: Parts of the underlying hash tree can be stored, while other parts can be calculated when necessary. This leads to various trade-offs between CPU utilization and memory usage during signing. Choosing an appropriate strategy and algorithm parameters is highly dependent on the hardware restrictions of the target platform. For example, a CPU constrained device (smart meter) would benefit from avoiding recomputing nodes, while a faster device can afford to.

Which Hash-Based Algorithms does ISARA support?

ISARA has implemented the leading candidates, HSS, XMSS, XMSS^MT and SPHINCS+, as part of our ISARA Radiate Quantum-safe Toolkit. By using our ISARA Catalyst OpenSSL Connector, you can create and sign digital certificates with these quantum-safe signature algorithms.

ISARA is also able to provide solutions and expertise for managing state, and specialized strategies for managing trees, which yield resource trade-off optimizations for given hardware requirements.

---

Technical Deep-Dive: More Information on Hash-based Algorithms

As mentioned before, the first construction, developed by Lamport, has the disadvantage that it is only a one-time signature scheme. As we will see, Merkle overcame this limitation and constructed a many-time signature algorithm by using binary trees and cryptographic hash functions.

One-Time Signature Schemes

A One-Time Signature (OTS) scheme is a set of three algorithms: one for generating one-time key pairs, one for computing one-time signatures, and one for signature verification. An instance of an OTS scheme has a specific key-pair (P, S), where P is the public key and S is the private (signing) key.

Both the OTS schemes and the Merkle trees (described below) use hash functions. An important question to ask is if the same hash function can be securely used for both types of constructions. And indeed, by including just a little extra data in each hash (this is called domain separation) we can essentially treat a single hash function as many distinct hash functions. In other words, if we use SHA-256 to generate the OTS instances, we can still securely use SHA-256 to construct the Merkle trees.

Many-time, or full, hash-based signature schemes use hash trees to efficiently combine many instances of an OTS scheme.

How does Hash-Based Cryptography Work?

We will now discuss how Merkle used binary trees—like the one shown in Figure 1—to combine many OTSs to create the public key of a many-time hash-based signature scheme. While the initial step of constructing the tree from these OTSs (which can be done offline) is usually slow in comparison to many other quantum-resistant constructions, signing is fast.

 

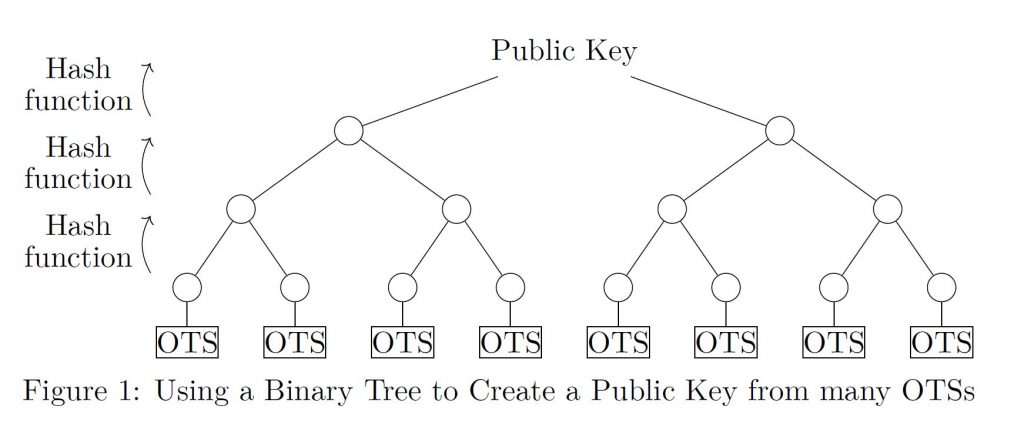
Binary Trees

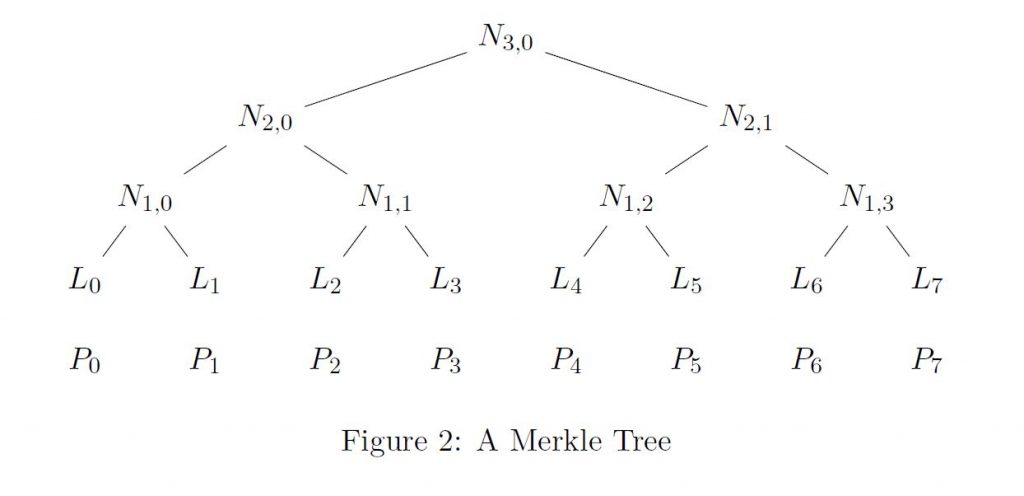
In a (perfect) binary tree all the nodes (except for the top node) come in pairs with a single node above them, and the distance from the bottom most nodes to the top-most is always the same. The node directly above another is its parent node, a node directly below a parent is its child node, and a pair of child nodes with the same parent are called sibling nodes. For example, in Figures 2 and 3, N_1,0 and N_1,1 are sibling nodes. They are also the child nodes of N_2,0 ; that is, N_2,0 is their parent node.

The top-most node is called the root node. The nodes on the bottom of the tree, which have no child nodes, are called leaf nodes. The leaf nodes are denoted L_{0 ,} . . . . , L₇ in Figure 2.

The level of a node is its distance from the bottom. By this we mean the leaf nodes have level 0, and the nodes N_j,i in Figure 2 have level j. The level of the root node, normally denoted h, is called the height of the tree. For example, the tree in Figure 2 has height 3. Merkle used binary trees to combine OTSs, More specifically: each leaf nodes comes from the public key of a (distinct) OTS instance, and every other node in the tree is calculated from its two child nodes. We will now describe how these nodes are calculated using a cryptographic hash function.

Cryptographic Hash Functions

Roughly speaking, a cryptographic hash function is a function that maps an arbitrary amount of data to a reasonably small, usually fixed length, output in a way where it is practically impossible to find an input that maps to a specific output (or two inputs that give the same output).

Intuitively, we can think of a Merkle tree as using hash functions to compress an ordered set of values into a single value, in a way where it is still easy to prove a value belongs to the original set. More concretely, a Merkle tree can be constructed from an ordered set P_{0 ,} . . . . , P_m of public keys of OTSs and a hash function H in the following way:

• Each leaf node is the hash output of an OTS public key. In other words, let the i^th entry in the bottom row be L_i = H(P_i); see Figure 2.
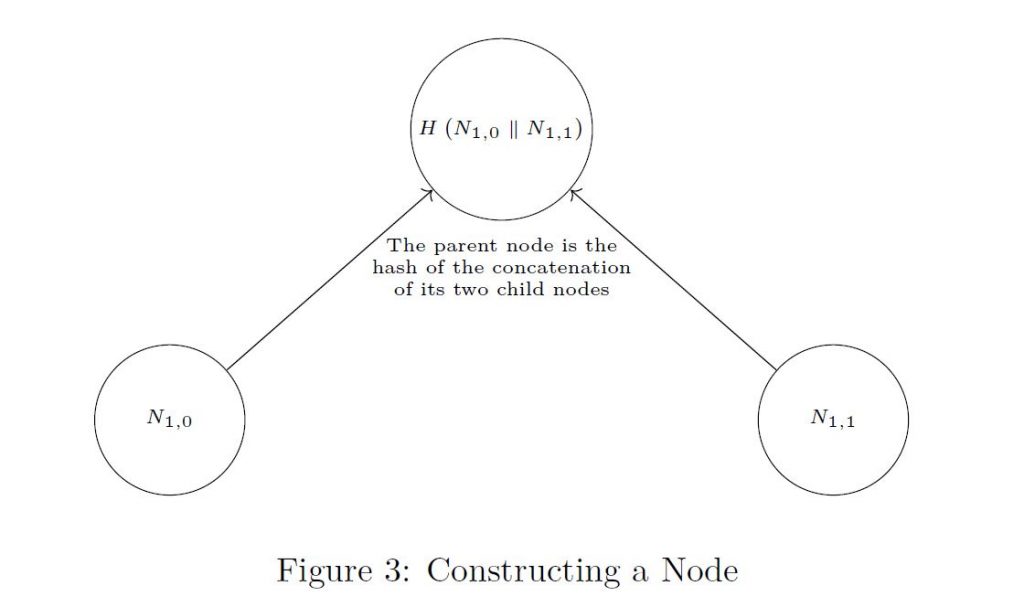
• Every other node in the tree is the hash of (the concatenation of) its two child nodes. For example, in Figure 3

N_1,0 = H(L₀ || L₁) and N_2,1= H(N_1,0 || N_1,1 );

where || denotes (bit-string) concatenation. (More generally, in Figure 3

N_1,i= H(L_2i || L_2i+1) and N_j+1,i= H(N_j,2i || N_j,2i+1).)

The public key of the Merkle signature algorithm is the root node. In Figure 2, the root node (public key) is N_3,0.

 

For a clearer picture of how to build a parent node, see Figure 3.

 

 

A hash tree is a generalization of a Merkle tree, where the P_ican be arbitrary data instead of OTS public-keys, see Figure 2.

As you cannot find the inverse of a hash function, it is practically impossible to find the nodes lower in the tree from nodes higher in the tree. Hence, it is impossible to find out information about the OTS signing keys given any set of nodes in the tree, in particular, given the root node.

Authentication Paths

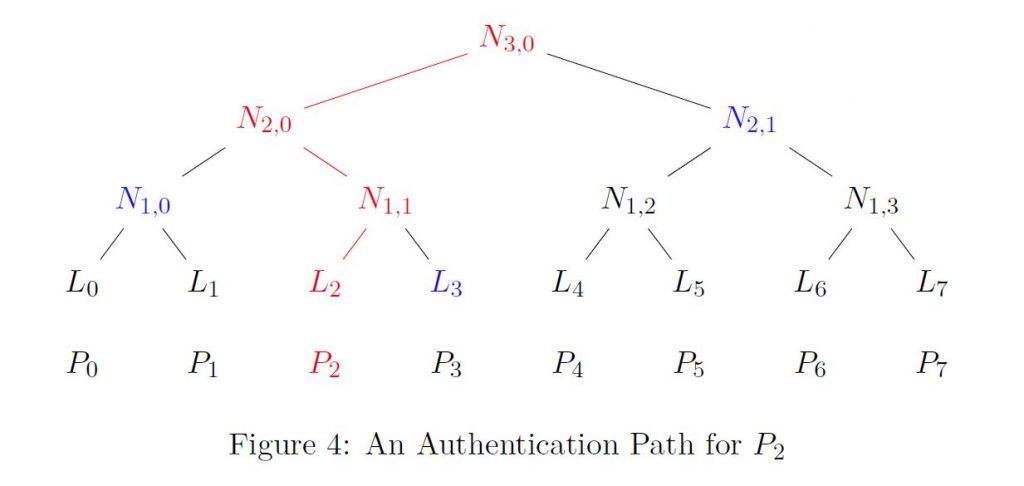
Notice that for any P_i that was used to create the Merkle tree, there is a unique path from the leaf node L_i to the root node (public key). For example, in Figure 4 the path from L₂ to the top is drawn in red. Given P_i, if you can construct a path of this form, then this proves with almost certainty that P_i was one of the values used to create the Merkle tree. This follows from the fact that it is computationally infeasible to find an input to H with a specific output, hence you cannot find nodes lower in the tree from nodes higher in the tree.

However, we actually use the sibling nodes of the leaf-to-root path nodes in order to check that the path was constructed legitimately. For this reason we introduce the notion of the authentication path of P_i, to be the ordered set of sibling nodes of the nodes in the path from L_i to the root node. In Figure 4, the authentication path (in blue) of P₂ is L_3, N_1,0, N_2,1. Given P_i(the public key of an OTS), and an authentication path for P_i, we can verify (authenticate) that P_icorresponds to a leaf node. That is, if P_iwas actually used in the generation of the tree, then it should be simple to reconstruct the path from P_ito the root node, given the authentication path.

Referring to Figure 4, we can prove that P₂ was use to create the public key of the Merkle tree given only its authentication path (in blue) L_3, N_1,0 , N_2,1 , by constructing a path from P₂ to the root node (public key).

To do this we just check that the values

• H(P₂),
• H(L₃|| H(P₂)),
• H(N_1,0 || H(L₃ || H(P₂))),
• H(N_2,1 || H(N_1,0 || H(L₃ || H(P₂))))

give a path where the last value H(N_2,1 || H(N_1,0 || H(L₃ || H(P₂)))) is the public key of the many-time signature algorithm (i.e., the root node). As P₂was actually used to construct the Merkle tree, H(N_2,1|| H(N_1,0 || H(L₃ || H(P₂)))) = N_3,0 by construction.

If the above calculation yields the public key, then we have proven P₂ was one of the OTS keys originally used to create the hash tree (because finding an illegitimate authentication path would require solving the computationally intractable problem of finding inverse images of a hash function).

Stateful Hash-Based Signature Schemes at a Glance

A generic construction for a many-time scheme is summarized below:

Secret Key Generation: Create m = 2^hOTS public/secret key-pairs (P_i, S_i). Intuitively, we can think of the secret key of the many-time scheme as the material needed to generate the OTS key-pairs.

Public Key Generation: Create the hash tree for P₁ , . . . . , P_m as described above. The root node is the public key of the hash-based signature scheme.

Signatures: To sign a message, choose an index i that has never been used before. Sign the message with S_i(the OTS signing key) to get the one-time signature _, and calculate the authentication path of P_i. The signature for the message is the one-time signature _, together with the authentication path of P_i.

Verification: To verify a signature on a message, we first run the onetime verification scheme using the message and _. Next, check that the authentication path of P_i gives a valid path from P_i to the public key of the hash-based signature (root node). If it does, accept the message and signature as authentic.

Time/Space Tradeoffs: As the tree can be regenerated from P₁ , . . . . , P_m , storing the entire tree is not always necessary. The decision of how much of the tree to store and how to manage the tree, leads to various CPU/memory tradeoffs. Moreover, all the keys P₁ , . . . . , P_mcan also be regenerated from a single short seed, further reducing the amount of long-term storage required.

Number of Signatures: If the tree has height h, then it can be used to sign up to 2^h messages.

Stateful Signatures: As each OTS signing key can be used at most once, in a stateful hash based signature scheme it is important to keep track of which one-time key-pairs have been used.

 

Bibliography

[1] David Cooper, Daniel Apon, Quynh Dang, Michael Davidson, Morris Dworkin, and Carl Miller. Recommendation for stateful hash-based signature schemes. Technical report, National Institute of Standards and Technology, 2019.
[2] Andreas Hülsing et al. SPHINCS+. NIST Round 2 Submissions for Post-Quantum Cryptography Standardization, 2019.
[3] A Hülsing, D Butin, S Gazdag, J Rijneveld, and A Mohaisen. XMSS: eXtended Merkle Signature Scheme. Crypto Forum Research Group RFC. rfc-editor.org/info/rfc8391, 2018.
[4] David McGrew, Michael Curcio, and Scott Fluhrer. Leighton-Micali hash-based signatures. Crypto Forum Research Group RFC. rfceditor. org/info/rfc8554, 2019.
[5] Ralph Merkle. Secrecy, authentication, and public key systems. Ph. D. Thesis, Stanford University, 1979.

 

---

Contact ISARA’s embedded security experts today

If you have further questions, set up a meeting with our team here.

---

Learn about the other five areas of math used in quantum-safe cryptography in our blog series, "Math Paths to Quantum-Safe Security":

• Isogeny-based cryptography
• Lattice-, code-, and multivariate-based cryptography to be posted